9433. Юбилейный торт

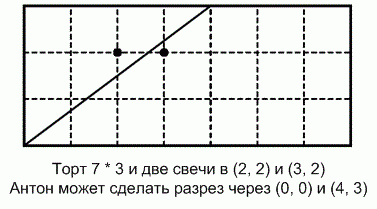
Два студента, Адам и Антон, празднуют двухлетнюю годовщину того, что не сдали экзамен по математической логике. После очень тщательного поиска в местном супермаркете они купили прямоугольный торт с целочисленными размерами и две свечи.

Позже в кампусе Адам вставил свечи в разные целые точки торта и дал Антону нож, чтобы тот разрезал торт. Разрез должен начинаться и заканчиваться целыми точками по краям торта, и он не должен касаться свечей. Также на каждом кусочке должна быть ровно одна свеча. Помогите Антону найти начальную и конечную точки разреза.

Вход. Одна строка содержит шесть целых чисел: w, h – размеры торта; a_x, a_y – координаты первой свечи; b_x, b_y – координаты второй свечи (3 ≤ w, h ≤ 10⁹, 0 < a_x, b_x < w; 0 < a_y, b_y < h; a_x ≠ b_x или a_y ≠ b_y).

Выход. Выведите четыре целых числа s_x, s_y, e_x и e_y – координаты начальной и конечной точки разреза. Обе точки разреза должны принадлежать сторонам торта.

Если решений несколько, выведите любое из них.

Пример входа	Пример выхода
7 3 2 2 3 2	2 0 3 3

РЕШЕНИЕ

конструктив

Анализ алгоритма

Рассмотрим координаты свеч A(a_x, a_y) и B(b_x, b_y). Если a_x ≠ b_x, то разрез можно провести отрезком с координатами (a_x, 0) – (b_x, h) :

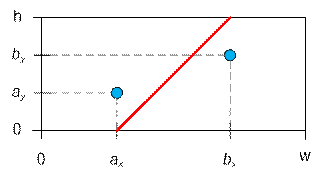
При a_x = b_x разрез можно провести отрезком с координатами (0, a_y) – (w, b_y) :

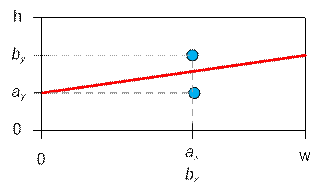
Реализация алгоритма

Читаем входные данные.

scanf("%d %d %d %d %d %d", &w, &h, &ax, &ay, &bx, &by);

Выводим ответ.

if (ax != bx) printf("%d %d %d %d\n", ax, 0, bx, h);

else printf("%d %d %d %d\n", 0, ay, w, by);